Why We Find AI in Nature
Artificial Intelligence is usually conceived as the manifestation of any non-human intelligence, this later one is described in opposition as “natural” intelligence.
Humans are not the only creatures living on earth which are capable of computing and demonstrating intelligence. Fortunately enough for us, human intelligence is usually regarded as – by far – the highest in their environment.
Nevertheless, other living creatures as insects or animals are known to demonstrate various forms of organizations and “collective” intelligence that fall into the Artificial Intelligence category.
In this article, we will see how powerful can be this Artificial Intelligence which does not involve any machines whatsoever but only biological species.
The idea of “intelligence” is, anyway an anthropomorphic notion, as we do not necessarily wish to conceive – or may not be able to conceive – anything different from our “human” intelligence. Therefore it stays a mysterious domain which is closely bound to the notions of information and organization and especially of “self-organization” which laws and principles are still a complete mystery for us.
The Ants: A Prodigious Source of Algorithms for Humans!
As everyone has probably observed himself or herself at least once in his/her life, ants demonstrate higher levels of an organization. Their perfect and impressive “armies” are able to gather in a very small amount of time any sort of food or material needed by the colony in extremely efficient ways. In fact, there is a very strong AI behind that and it is only relatively recently (1989) that it had been uncovered.
The Ant Colony Optimization Algorithms
In a nutshell, scout ants will randomly walk outside the colony and signal food by leaking pheromones trails. Other ants which will be next to the trails will be attracted by it and will collect food and reinforce the trail by leaking more pheromones.
Since pheromones are volatiles, only the shortest trail will end in becoming selected.
The evaporation of pheromones is the way to constantly remove the bad solutions to the optimization problem ( finding the shortest path between the colony and the food )
Initially, the ant colony algorithm was studied in 1989 by the biologists S. Goss, S. Aron, J.-L. Deneubourg et J.-M. Pasteels as a description of a self-organized system.
From the original algorithm, a lot of “man-made” computers algorithms were created, becoming more and more complex with the years. The ants are been modeled as “abstract” agents which are searching for a solution(s) of given optimization problems using individual heuristic processes (so the whole system is called meta-heuristic).
So, starting with the original A.I algorithm observed in nature, several “ant colony” algorithms were created by computer scientists and mathematicians. They belong now to a more general class of algorithms called the Swarm Intelligence algorithms.
Here we represent the basics of the ant colony optimization algorithm as found in nature.
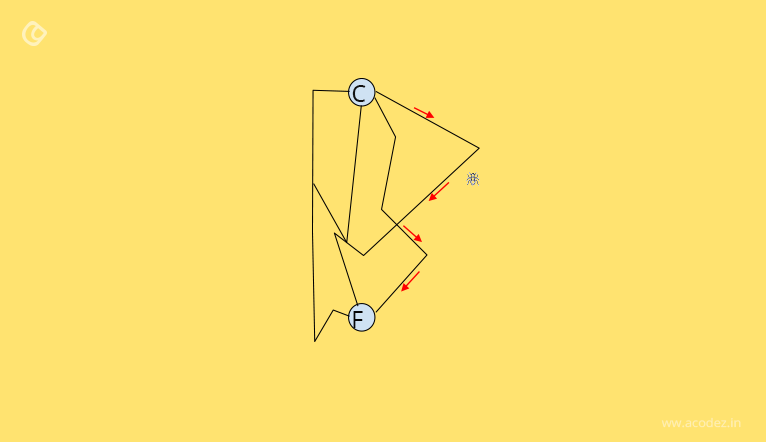
Step 1: A scout ant will initially signal the presence of food (F) to the nest of the colony (C) by leaking pheromones (red arrows) on the trail that the ant discovered.
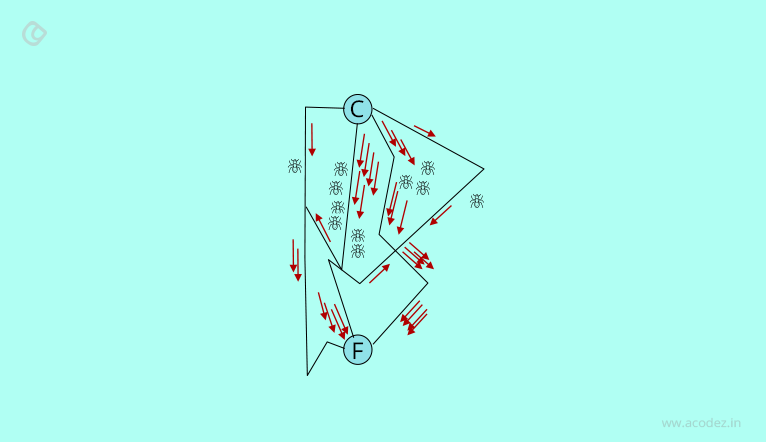
Step 2: Following the initial marking, other ants will explore other paths that lead to the food sources and leak pheromones as well on the trail they follow, as a reinforcement. The more pheromone, the more attractive is the trail and the more ants will “travel” through it. In parallel, other scout ants will explore new paths.
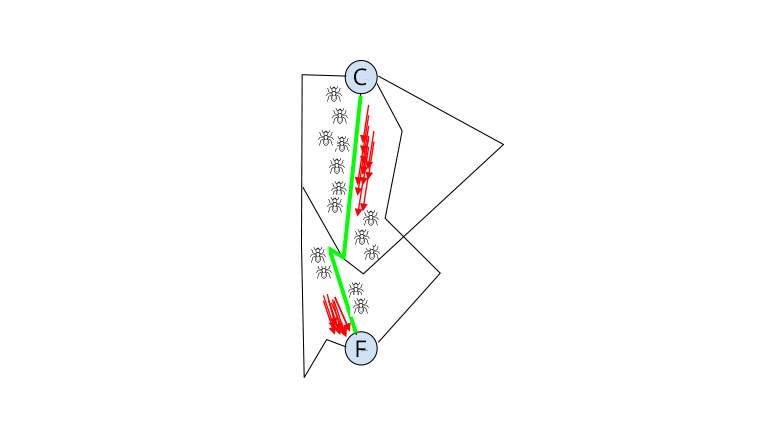
Step 3: Because the pheromones will evaporate after a certain amount of time, only the shortest path will remain and this is the path that the ants will take to bring the food to the colony. In other terms, only the most “popular” trail will survive the evaporation of pheromones.
When Darwinism Leads to the Evolutionary Algorithms
The mechanisms of evolution, and in particular the Darwinist theory have been studied for several centuries. The observation of the way some populations evolve to become the fittest category has been the start for a new class of algorithms called the Genetic Algorithms belonging to a more generic category, the Evolutionary Algorithms.
The most straightforward evolutionary algorithm are the ones which have been borrowed from the natural selection mechanisms: the Genetic Algorithms.
The Genetic Algorithms
In nature, a population has offspring which inherits the characteristics of their parents. These characteristics will be added to the next generation. If the parents have better fitness, then the offspring is better than the parents and have a better chance, as well, of surviving.
This is the concept of natural selection as found in nature.
From that, the Genetic Algorithms were created which aim at formalizing- in terms of computer science – that natural concept.
A genetic algorithm will usually consist of 5 phases:
- Initial population phase
- Fitness function selection phase
- Selection phase
- Crossover phase
- Mutation phase
Phase 1: Population
We consider a population P which consists of N individuals P1,…, PN.
Each individual is characterized by their chromosomes C. This is a string from a fixed alphabet named the genes. For example, if we consider the genes to be the alphabet A-Z, a chromosome will consist of a normal word:
C = AWDFRTGHUNJMKLOPSET
In nature, the alphabet consists of all the possible triples among the set of letters {A, G, C, T}. A gene is, therefore, a three-letter word such as AGC or GAT or GGC.
In the Genetic Algorithms, the alphabet is usually binary. So chromosomes will be represented by binary sequences.
Phase 2: Fitness Function
The next phase consists of defining a fitness function. That function will return a score to each individual of the population which will indicate how that individual is able to compete with other individuals regarding a set of constraints.
The higher the score is, the higher the probability is that the individual will be selected for reproduction.
Phase 3: Selection
The selection phase consists in choosing the fittest individuals based on their fitness score. Parents are then selected so they pass their genes to the next generation.
Phase 4: Crossover
During reproduction, a crossover point (in orange) is chosen randomly in the chromosome structure.
| P1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
↑↓ |
↑↓ |
↑↓ |
↑↓ |
↑↓ |
↑↓ |
↑↓ |
↑↓ |
↑↓ |
↑↓ |
↑↓ |
|
|
|
|
|
|
|
|
|
| P2 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
The two parents, P1 and P2, will have offspring resulting from the exchange between each other of the genes up to the crossover point. This will give a new population of 2 individuals P1’ and P2’.
| P1’ |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| P2’ |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
Phase 5: Mutation
Some offspring may be subject, with low probability, to mutation. This means some of their genes may be flipped.
For instance instead of getting the following chromosome:
| P1’ |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
They will get this one:
| P1’ |
0 |
0 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
Convergence to a Solution
The algorithm will converge to a solution when the population has converged, meaning that there are no more significant differences between the offspring and their parents. The population always stays at the fixed size of N, for example, the parents(s) die after the offspring is generated(2) or the least fitted individuals die so to equilibrate the population.
Example
Here we aim at showing a concrete implementation and use of the Genetic Algorithms.
We consider a fitness function f returning the numbers of 1’s in the chromosome. For example, f([11001001])=4 and we consider the chromosome to have fixed length 8.
Our goal is to reach a state where the population will have the maximal possible fittest score, ideally, all individuals in the population have a score of 8.
The following C# code provides an implementation of the basic genetic algorithm and can solve the aforementioned problem.
First, we write a few routines that will generate random data:
using System;
using System.Collections.Generic;
using System.IO;
using System.Linq;
using System.Security.Cryptography;
using System.Text;
using System.Threading.Tasks;
namespace Genetic2 {
class Program {
static int N = 100;
static RNGCryptoServiceProvider rngCsp = new RNGCryptoServiceProvider();
static byte[] buffer = new byte[1];
enum gene {
zero = 0,
one = 1
};
static int generateRandomNumber(int n) {
rngCsp.GetBytes(buffer);
return (Convert.ToInt32(buffer[0]) % n);
}
static gene generateRandomGene() {
rngCsp.GetBytes(buffer);
return (gene)(buffer[0] & amp; 0x01);
}
static gene[] generateRandomChromosome() {
gene[] g = new gene[8];
for (int i = 0; i & lt; 8; i++) {
g[i] = generateRandomGene();
}
return g;
}
static int generateCrossover() {
rngCsp.GetBytes(buffer);
return (Convert.ToInt32(buffer[0]) % 8);
}
We define as well the class individual for the individuals that will be part of the population
They contain several parameters that can tell who are their parents, if they are dead or alive (at a given generation) or if they are currently being selected for reproduction.
The parents are just a structure containing two individuals.
Here there is no notion of sex so the population is hermaphrodite.
class individual
{
public string id;
public gene[] chromosome;
public string parent1_id;
public string parent2_id;
public int n_generation;
public int reproduced;
public bool alive;
public float mutation_rate;
public bool selectedForReproduction;
}
struct parents
{
public individual parent1;
public individual parent2;
};
We maintain the generations inside a global array named hist_populations.
It contains the populations of the N individuals for each generation.
The whole set of generated individuals is maintained in an array named global_population. That array will list any individuals who have been created even if that individual is not alive.
//the population of the n^th generation e.g those who survive
static individual[][] hist_populations= new individual[1000][];
//the entire population included the eliminated individuals
static List<individual> global_population = new List<individual>();
static int curr_generation=0;
static List<parents> list_parents;
This init function initializes the initial population. The initial population has no parents and possess random chromosomes.
public static void init() {
// assign random genes
for (int i = 0; i < N; i++) {
individual ind = new individual();
ind.id = “”+i;
ind.chromosome = generateRandomChromosome();
ind.n_generation = 0;
ind.alive = true;
ind.reproduced = 0;
ind.selectedForReproduction = false;
global_population.Add(ind);
hist_populations[0] = global_population.ToArray();
}
}
The getMaxScoreRate function will compute the amount of the current population that possess maximal fitness. The closer we get to 1, the closer we are to the solution of the problem and the end of the evolution.
static float getMaxScoreRate(int gen) {
int max = hist_populations[gen].Max(ind_ => fitness(ind_));
int S = 0;
for (int i = 0; i < N; i++) {
individual ind = hist_populations[curr_generation][i];
if (fitness(ind) == max) {
S++;
}
}
return (float)(S / N);
}
- The fitness function will return a fitness score, here the number of 1’s in the chromosome of an individual.
- The getWeakest function will return the index of the first element of the weakest individuals of the population, in terms of their fitness function.
- The eliminateWeaks function will mark as non-alive the N/2 individuals which are weaker than the other N/2 individuals of the total population. This is a mechanism of selection. The N/2 individuals eliminated make room for the N/2 new individuals of the new generation. This is obviously a fundamental function otherwise there would be no possible convergence to the fittest population. Such “raw” selection exists in nature, in wildlife for instance, where the weakest animals are not allowed to survive and die from diseases or killed by stronger animals. In our algorithm, there is no notion of “age” but obviously, an individual from a previous generation will see his chance of staying alive diming and diming since his chromosomes are becoming weaker and weaker than the others.
static int fitness(individual ind) {
gene[] chromosome = ind.chromosome;
int score = 0;
for (int i = 0; i < 8; i++) {
score += (int) chromosome[i];
}
return score;
}
static int getWeakest() {
int min = hist_populations[curr_generation].Where(ind_ => ind_.alive == true).Min(ind_ => fitness(ind_));
for (int i = 0; i < N; i++) {
individual ind = hist_populations[curr_generation][i];
if ((fitness(ind) == min) && (ind.alive == true)) {
return i;
}
}
//should never ever happen
return– 1;
}
static individual getIndividualByID(String id_) {
foreach(var ind in global_population) {
if (id_.Equals(ind.id))
return ind;
}
return null;
}
static void eliminateWeaks() {
//we eliminate the least fittest individuals of the population
//so they will not be allowed to reproduce themselves
//half of the population needs to be eliminated
//since parents will duplicate themselves
for (int j = 0; j < N / 2; j++) {
int wi = getWeakest();
hist_populations[curr_generation][wi].alive = false;
getIndividualByID(hist_populations[curr_generation][wi].id).alive = false;
}
}
The reproduce function is the most important of all. It implements the reproduction mechanism.
First, we call eliminateWeaks() so we remove the N/2 weaker individuals.
We generate the parents randomly by calling generateParents() so we create pairs of individuals in the remaining N/2 strongest population.
The pair of parents, individuals selected for reproduction, is contained in the list_parents variable.
The reproduction itself consists of performing the crossover with the two chromosomes of the parents, e.g mixing them using the crossover line.
For each pair of parents, we get two new individuals, namely offspring1 and offspring2.
The population of the new generation consists of the N/2 parents – which are reverted back to a condition of “normal” individuals and unmarked for reproduction – and the N/2 offspring population.
Note that here we did not implement a mutation function for the sake of simplicity.
static void reproduce() {
eliminateWeaks();
//the remaining population will start the “new generation” population
//each parents are selected randonmly
generateParents();
curr_generation++;
hist_populations[curr_generation] = new individual[N];
//crossover is generated and two new individuals are generated
//now let us have the parents generate new individuals!
int j = 0;
foreach(parents p in list_parents) {
int c = generateCrossover();
gene[] ch1 = p.parent1.chromosome;
gene[] ch2 = p.parent2.chromosome;
gene[] off1 = new gene[8];
gene[] off2 = new gene[8];
for (int i = 0; i <
c; i++) {
off1[i] = ch1[i];
off2[i] = ch2[i];
}
for (int i = c; i < 8; i++) {
off1[i] = ch2[i];
off2[i] = ch1[i];
}
individual offspring1 = new individual();
individual offspring2 = new individual();
offspring1.alive = true;
offspring1.chromosome = off1;
offspring1.id = “”+(global_population.Count + 1);
offspring1.mutation_rate = 0;
offspring1.parent1_id = p.parent1.id;
offspring1.parent2_id = p.parent2.id;
offspring1.reproduced = 0;
offspring1.selectedForReproduction = false;
global_population.Add(offspring1);
hist_populations[curr_generation][j] = offspring1;
j++;
offspring2.alive = true;
offspring2.chromosome = off2;
offspring2.id = “”+(global_population.Count + 1);
offspring2.mutation_rate = 0;
offspring2.parent1_id = p.parent1.id;
offspring2.parent2_id = p.parent2.id;
offspring2.reproduced = 0;
offspring2.selectedForReproduction = false;
global_population.Add(offspring2);
hist_populations[curr_generation][j] = offspring2;
j++;
p.parent1.reproduced = p.parent1.reproduced++;
p.parent2.reproduced = p.parent2.reproduced++;
p.parent1.selectedForReproduction = false;
p.parent2.selectedForReproduction = false;
hist_populations[curr_generation][j] = p.parent1;
j++;
hist_populations[curr_generation][j] = p.parent2;
j++;
}
}
private static void generateParents() {
list_parents = new List <
parents > ();
//pick up randomly pairs in the live population of the current generation
while (list_parents.Count < N / 4) {
parents p;
int i = generateRandomNumber(N);
while ((hist_populations[curr_generation][i].alive == true) && (hist_populations[curr_generation][i].selectedForReproduction !=
false)) {
i = generateRandomNumber(N);
}
p.parent1 = hist_populations[curr_generation][i];
hist_populations[curr_generation][i].selectedForReproduction = true;
int j = generateRandomNumber(N);
while ((hist_populations[curr_generation][i].alive == true) && (hist_populations[curr_generation][j].selectedForReproduction !=
false)) {
j = generateRandomNumber(N);
}
p.parent2 = hist_populations[curr_generation][j];
hist_populations[curr_generation][j].selectedForReproduction = true;
list_parents.Add(p);
}
}
The Main routine will iterate call to reproduce()until that, either the population converges, meaning that the rate of the population having maximal fitness is at least 90%, either the maximal amount of generations is reached and so there is no convergence.
We should have used an approach where we make sure the rate of the population stays superior at 90% after a given generation, for a significant amount of generations. Here we reach a rate of 100% so there is no need for such verifications.
static void Main(string[] args)
{
init();
while (getMaxScoreRate(curr_generation) < 0.9)
{
if (curr_generation>999)
{
Console.WriteLine(“cannot converge to a solution current max score is “ + getMaxScoreRate(curr_generation));
return;
}
reproduce();
}
Console.WriteLine(“converge to a solution current at generation “+curr_generation+” max score is “ + getMaxScoreRate(curr_generation));
string hist = “”;
for(int i=0;i<curr_generation;i++)
{
hist += i + “;” + getMaxScoreRate(i) + “\n”;
}
File.WriteAllText(“hist.csv”, hist);
}
}
}
The result of this very basic genetic algorithm can be visualized in a chart that displays the rate of the population having maximal fitness for each new generation.
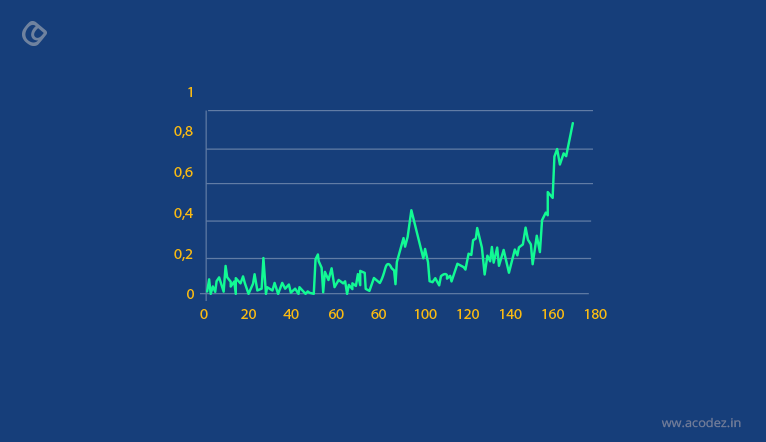
As we can see we need to wait for around 200 generations to obtain a convergence… This is the traditional slowness of evolution!
The genetic algorithms created by computer scientists are much more sophisticated than our small example but the principle stays the same which is at the base of the evolution and natural selection as observed in nature.
The Evolutionary Algorithms
The Evolutionary Algorithms makes extensive use of Evolution strategies, Differential Evolution or Neuro-Evolution. They are an ongoing and fascinating field of research, especially because they often appear weaker than complex evolution mechanisms found in nature. For instance, the evolution mechanisms of a fertilized egg are incredibly more complex than what the best evolution algorithms created by scientists could offer.
One of the critics often heard against these class of A.I is that it is still quite slow and converge very slowly to a solution.
Nevertheless, they are used with certain success in various fields. For example, the evolved antennas. These are radio-communication antennas designed by a computer programmed with evolutionary mechanisms.
Here we present an example of such an evolved antenna:

Of Bees and Octopuses
The Artificial Bees Colony Algorithm

The artificial bee colony algorithm (ABC) is inspired by the intelligent foraging behavior of bees.
Foraging is the main – if not the only – reason of existence for bees and so as a vital and critical process for the survival of their colonies, a self-organization algorithm “auto-developed” itself which we will describe now:
A bee colony, besides the queen, consists generally in the following population, representing the division of labor:
- Unemployed foragers (UNF)
- Employed Foragers (EMF)
- Experienced foragers (EXF)
The unemployed foragers itself falls into two categories:
- The Scout bee (S)
- The Recruit bee (R)
The foraging algorithm of the bees can be described as such:
Scout Bees Search for Sources of Nectar
The scout bees S will search randomly for nectar sources. Once found, the fitness of that source is evaluated by the bee. The bee returns to the hive and starts at a special location of the hive, the so-called “Waggle” dance.
That dance is in fact a signal that contains all the information needed to evaluate the nectar source in terms of distance, orientation, and value.
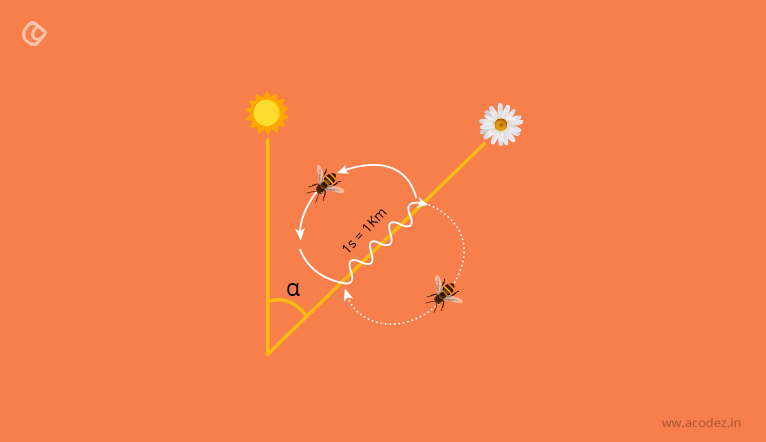
That dance is employed by unemployed bees. If the onlooker bees “like” the dance ( the information provided by the dance), these bees will go to the source to collect nectar. The dance will be more frequent if the quality of the source is good and so more onlooker bees will join that source, becoming employed bees.
If the source becomes exhausted, the formerly employed bees become scout bees and so on.
Here we see that the algorithm permanently moves bees from one working category to another.
The ABC algorithm
The ABC algorithm formalizes the A.I of the bees as observed in nature.
In this algorithm, there is only one employed bee for each source of food. The position of the sources and the fitness function associated with these sources are solutions of an optimization problem. The behavior of the abstract bees is slightly different from the behavior of the “real” bees but the principle stays roughly the same.
The algorithm and all its applications are described in the ABC official website.
Why Octopuses May be the Future of AI in Robotics

It may be surprising to you but octopuses are potentially one of the most “non-human” intelligent creatures on earth. Researchers are still trying to figure it out whether octopuses have real cognitive intelligence or not but studies from the behavior of octopuses have already inspired researchers in robotics.
Interestingly enough, an octopus has three hearts, nine brains, and blue blood! This explains why the potential intelligence of such an animal should be far, far away from the human representation of intelligence.
The (potential) intelligence of octopuses falls into the AI category since it is totally a non-Human intelligence ( the octopuses are not – usually- domestic animals unlike dogs for instance )
Octopuses are able among others:
- To learn how to get out of mazes;
- To use tools;
- To navigate using landmarks;
- To open “ childproof bottle” very fast;
- They can open Jars from the inside;
- They can escape tanks and find their way back to the ocean.
Yet there are still no formal proof of a real cognitive intelligence of the octopuses but the mechanism behind octopus brain behavior is starting to inspire many researchers…
In the paper “The Octopus as a Model for Artificial Intelligence A Multi-Agent Robotic Case Study” , the “curious” ability of octopuses to solve distributive problems is explored as an alternative to the human brain.
Immunity and Brains

Artificial Immune Systems
The artificial immune system (AIS) is a branch of biologically inspired computing and immunocomputing.
Same as for the other algorithms presented in that article, its functioning is inspired by the vertebrate immune system.
It falls into 4 categories:
- Clonal Selection Algorithm;
- Negative Selection Algorithm;
- Immune Network Algorithms;
- Dendritic Cell Algorithms.
These algorithms are very specialized and we mention them only for information.
Biological Neural Networks inspired AI
The functioning of the biological neural networks has inspired artificial neural networks algorithms.
The Artificial neural networks are far less complex than their biological counterparts.
Yet they are powerful tools to solve many problems in machine learning.
The literature on the subject is very important and artificial neural network is probably the most popular artificial intelligence algorithms taught in many schools, institutes, and universities.
We only aim at presenting quick facts, only to give an overview.
- The artificial neural network is made of elementary units called artificial neurons;
- The artificial neurons (neurons) can receive a signal, process it and eventually; signal other connected neurons;
- Neurons are connected via edges. A weight system calibrates the signals between neurons. The output of a neuron is a nonlinear function of the sum of inputs.
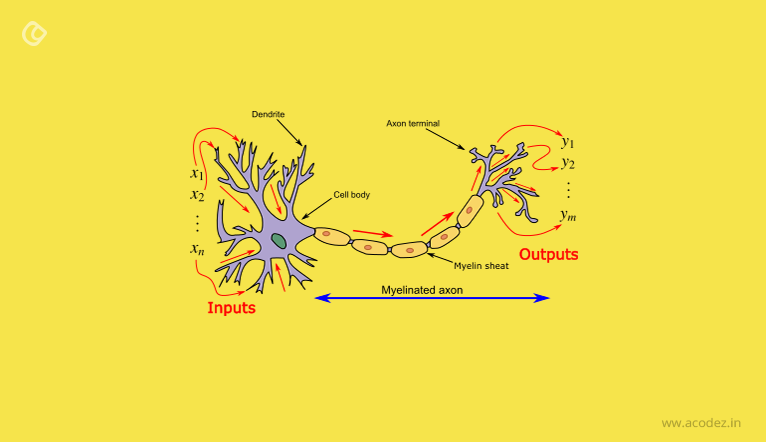
Here we present, to illustrate the topic, the connection between two real neurons as observed in nature:
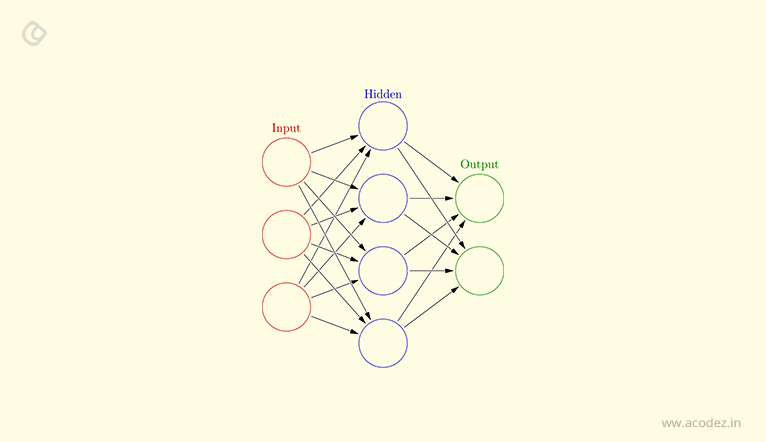
And the connections between artificial neural networks :
What We Know About Swarms, Packs and Flocks, and Other Things
We have just been looking in this article at the surface of the artificial intelligence found in nature. The algorithms observed for ants or bees, called swarm algorithms exist also for termites or bedbugs for instance.
Even insignificant creatures such as bedbugs do have a “collective” A.I which allows them to locate their prey and prevents these bedbugs to be caught.
- Pack of rats has A.I.
- A flock of birds or fishes have A.I.
There exists even a family of creatures, mostly unknown to the average reader, called the Physaliida. These creatures are in fact micro-creatures of different shapes and quantity, forming together a giant artificial creature (“a living vessel”). The mechanism of formation and organization of that “vessel” is as well an artificial intelligence.
There exists much more example of artificial intelligence found in nature and used every day by computer scientists. In fact, there are so much of these algorithms than we may think one of these days if we should not reverse the terminology, naming these algorithms “natural intelligence” and calling our intelligence … The artificial Intelligence.
Once again, man, in his ignorance thinks he is the center of all things. We learned that our planet is not the center of the universe and that it is “just” one of the planets revolving around a sun. We learned that we were the product of an evolution involving primates. We may soon learn that our intelligence is not the biggest intelligence in the universe and that there do exist many other bits of intelligence, comparable to ours, but simply different in goals.
AI is a very popular term nowadays, a “buzzword”. The next frontier to reach is to understand what means truly “intelligence” and what is at the root of all these algorithms observed in nature. This is the real challenge to come for courageous men (and women) of science!
Acodez is a prominent web design and web development company in India offering all kinds of website design and development solutions at affordable prices. We are also an SEO and digital marketing agency offering inbound marketing solutions to take your business to the next level. For further information, please contact us today.
Looking for a good team
for your next project?
Contact us and we'll give you a preliminary free consultation
on the web & mobile strategy that'd suit your needs best.



















this is really amazing blog for me i learn so many important things from the nature and today i get to know that we can learn lot from the nature including AI algorithm